Innovación para la enseñanza de la Química

VTOS: VISUALIZADOR TRIDIMENSIONAL DE OPERACIONES DE SIMETRÍA PARA EL GRUPO PUNTUAL D₂

Rosa Elena Arroyo-Carmona¹, Hugo Vázquez-Lima², Samuel Hernández-Anzaldo², Yasmi Reyes-Ortega², Aarón Pérez-Benítez¹

1-Facultad de Ciencias Químicas. Benemérita Universidad Autónoma de Puebla. 18 sur y av. San Claudio. Col. Jardines de San Manuel. C. P. 72570, Puebla, Pue. México.

2-Centro de Química del ICUAP. Benemérita Universidad Autónoma de Puebla. 18 sur y av. San Claudio. Col. Jardines de San Manuel. C. P. 72570, Puebla, Pue. México.

E-mail: aaron.perez@correo.buap.mx

Recibido: 10/07/2020. Aceptado: 28/07/2020.

Resumen. Se describe la construcción y el uso de un modelo tridimensional sencillo que es útil para visualizar las operaciones de simetría del grupo puntual D₂, al que pertenecen entidades químicas tales como el (C₂₈-D₂)[5,6]-fullereno y el catión complejo [Cu(en)₂]²⁺. El modelo puede construirse con materiales reciclables o de costo bajo y las operaciones de simetría sirven de base teórica para su diseño. Los ejes binarios de rotación propia se indican mediante las notaciones convencional y matricial a dos renglones de la teoría de permutaciones. Por ser un grupo puntual de orden cuatro, el D₂ es ideal para introducir conceptos básicos de la teoría de grupos, tales como el de "tabla de multiplicación" y grupo Abeliano.

Palabras clave. simetría molecular, grupo Abeliano, modelo tridimensional, grupo puntual D₂.

VTOS: three-dimensional visualizer of symmetry operations for d₂ point group

Abstract. The construction and use of a simple 3D-model that is useful for visualizing the symmetry operations of D₂-symmetry point group are presented. (C₂₈-D₂)[5,6]-fullerene and [Cu(en)₂]²⁺ complex cation belong to this symmetry point group. The model can be built starting from low-cost or recyclable materials and the symmetry operations serve as a theoretical basis for its design. Because it is a point group of order four, D₂ is ideal for introducing basic concepts of group theory, such as "multiplication table" and the Abelian group.   

Keywords. molecular symmetry, Abelian group, three-dimensional model, D₂ point group.

INTRODUCCIÓN

La simetría y su uso en la química, la física y las matemáticas, así como en la vida cotidiana son muy comunes. No obstante, la enseñanza y el aprendizaje requieren del uso de la inteligencia espacial del alumno, quien en ocasiones necesita un modelo tridimensional para desarrollarla. En el caso de la química usualmente recurrimos a imágenes de moléculas y modelos computacionales o físicos para ilustrar las operaciones y los elementos de simetría que poseen (Cotton, 1999; Hargittai y Hargittai, 2009).

Así, en nuestros cursos de estereoquímica orgánica y de química de coordinación, utilizamos modelos físicos de bajo costo desarrollados por nosotros mismos y por nuestros estudiantes, para la enseñanza y el aprendizaje de los conceptos fundamentales de la simetría. Básicamente se han seguido dos estrategias: la primera es abordar ejemplos de alta simetría (Pérez-Benítez y Arroyo-Carmona, 2003) y la segunda usar ejemplos de baja simetría (Pérez-Benítez, 2002).

En este trabajo se presenta con el mismo objetivo, una tercera estrategia que consiste en el estudio de la simetría del grupo puntual diédrico D₂ (Fuentes, 2008), a partir de un modelo elaborado a base de un rectángulo de cartón corrugado. A este modelo lo hemos denominado genéricamente como "Visualizador Tridimensional de Operaciones de Simetría, VTOS".

Al grupo puntual D₂ pertenecen entidades químicas como el (C₂₈-D₂)[5,6]-fullereno (Cozzi, Powell y Thilgen, 2005) y el catión complejo [Cu(en)₂]²⁺ (Figura 1).

(a)

(b)

Figura 1. Vista colineal a los tres ejes de rotación propia C₂ del (C₂₈-D₂)[5,6]-fullereno (a) y la ubicación de los tres C₂ del catión complejo [Cu(en)₂]²⁺, siendo C_2z el eje principal (b).

EL GRUPO PUNTUAL DE SIMETRÍA D₂

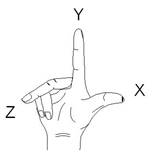
Los objetos y las moléculas que pertenecen a este grupo puntual son de orden cuatro (h = 4); es decir, poseen cuatro operaciones propias de simetría: La identidad (E) y tres rotaciones C₂ (giros de 180°) que normalmente coinciden con los ejes cartesianos (C_2x, C_2y y C_2z), los cuales se ilustran en la figura 2a siguiendo la regla de la mano derecha (Tipler, 2006).

Si consideramos un objeto rectangular cuasi-plano al que le dibujamos un círculo en la esquina superior izquierda y le aplicamos independientemente, rotaciones de 180° en el eje X, en el eje Y y en el eje Z, vemos en los dos primeros casos que el punto se ha desplazado respectivamente, a la esquina inferior izquierda y superior derecha de la parte de atrás; en cambio, una rotación en el eje Z (perpendicular al plano del papel) desplaza el punto a la esquina inferior derecha de la parte de enfrente (Figura 2b).

A falta de más puntos, esos movimientos que se han aplicado sobre el objeto son distinguibles. Ese hecho se debe a que el rectángulo modificado ya no es muy simétrico; así que si ahora dibujamos sobre el modelo inicial, puntos en los sitios que generamos con las rotaciones; es decir, dos puntos en la esquina superior izquierda e inferior derecha por la parte de enfrente y dos puntos en la esquina superior derecha e inferior izquierda por la parte de atrás, entonces generamos un objeto con más simetría.

(a) (b)

Figura 2. Ejes cartesianos (a) y notación de los puntos que se usarán en el modelo (b).  Rotaciones de 180° aplicados en X, Y y Z, sobre un punto contenido en un rectángulo cuasi-plano (c – e). R_z es la rotación en el eje perpendicular al plano del cartón.

Con esos cuatro puntos ya se pueden definir las operaciones de simetría del grupo puntual D₂ que son: tres ejes binarios de rotación propia C₂ (colineales con los ejes cartesianos X, Y y Z y que por lo tanto se denominaron en este contexto como C_2x, C_2y y C_2z) y la identidad E (Figura 3). En esa figura se observa que todas las operaciones de simetría dan aparentemente el mismo resultado porque obviamente eso son: ¡Operaciones de simetría!

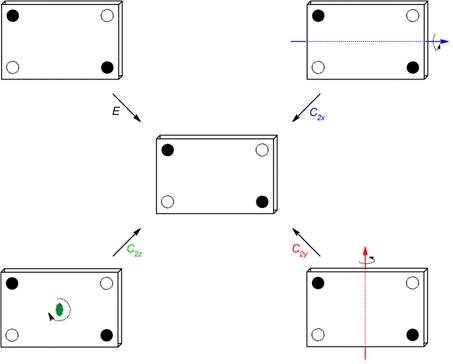
Figura 3. Operaciones de simetría del grupo puntual D₂: La identidad E y tres ejes binarios de rotación propia C₂ colineales con los ejes cartesianos X, Y y Z.

Para matizar el resultado de aplicar cada una de esas operaciones se pueden enumerar los puntos según se indica en la Figura 4. La matriz abajo de las flechas indica, según la notación a dos renglones para las permutaciones (Bogart, 2017), como se intercambian los puntos al aplicar la operación de simetría correspondiente; por ejemplo, C_2x hace que permuten 1 con 4 y 2 con 3 (Figura 4a).

En las tablas de multiplicación de los grupos puntuales, las operaciones de simetría del grupo se enlistan en las cabeceras, iniciando con las propias y continuando con las impropias. Asimismo, el orden establecido para la multiplicación es:

a_i b_i = c_i

donde a_i es la operación en la cabecera de la columna, b_i es la operación en la cabecera del renglón y c_i es el producto de las operaciones de simetría (Tabla 1; Willock, 2009). Estos hechos permiten demostrar las propiedades matemáticas del grupo; por ejemplo, que:

1) Las operaciones de simetría nunca se repiten en un renglón ni en una columna

2) Se cumple la propiedad de cerradura: El producto de dos operaciones de simetría es una operación que también forma parte del grupo.

3) A menos que se trate de un grupo Abeliano (Fuentes y Fuentes, 2008), el orden en el que se aplican las operaciones de simetría puede dar un resultado distinto.

4) La operación identidad E es una operación neutra por lo que siempre deja invariante a cualquier otra operación del grupo.

Figura 4. Resultado de aplicar las operaciones de simetría del grupo puntual D₂ usando puntos numerados sobre el modelo propuesto y la notación a dos renglones de la teoría de permutaciones.

En la figura 5 se demuestra que el grupo puntual D₂ es Abeliano; es decir, que sus operaciones de simetría son conmutativas. Así:

C_2z = C_2xC_2y = C_2yC_2x

Tabla 1. Tabla de multiplicación del grupo puntual D₂, un grupo Abeliano de orden cuatro (h = 4)

	E	C2x	C2y	C2z*
E	E	C2x	C2y	C2z
C2x	C2x	E	C2z	C2y
C2y	C2y	C2z	E	C2x
C2z	C2z	C2y	C2x	E

*Por convención, C_2z se denomina eje principal y es perpendicular al plano molecular; en nuestro caso, al plano del cartón.

Construcción del Visualizador de Operaciones de Simetría, VTOS, para el grupo puntual D₂

Materiales:

Un rectángulo de cartón corrugado de 7 x 10 cm

4 etiquetas o círculos de papel de un mismo color

Tres hisopos o seis palillos de madera

Procedimiento:

1) Dibuje o coloque las etiquetas sobre el cartón, según se ilustra en la figura 3; es decir, en las esquinas superior izquierda e inferior derecha de cada lado del cartón.

2) Divida los hisopos en dos e introdúzcalos intersectando la mitad de las aristas del rectángulo, según se ilustra en las figuras 4 y 6b.

3) Inserte el tercer hisopo (o palillo) en el centro del rectángulo, perpendicularmente al plano del cartón. Si es necesario, use un punzón para hacer un orificio inicial y facilitar el ingreso del hisopo. El modelo terminado se presenta en la figura 6b.

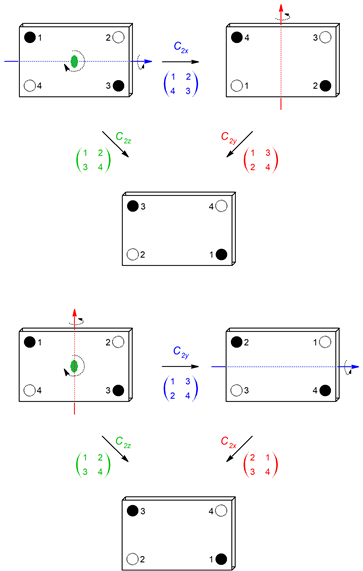
Figura 5. Demostración de la propiedad conmutativa del producto de dos operaciones de simetría en el grupo puntual D₂: C_2z = C_2x C_2y = C_2y C_2x

(a)

(b)

Figura 6. Materiales (a) y modelo terminado del VTOS para el grupo puntual D₂ (b).

Ejercicio sugerido (Trabajo colaborativo)

Los objetos que pertenecen a este grupo puntual son quirales (del griego chair = mano), lo cual significa que el objeto y su imagen en un espejo plano no son superponibles entre sí (Thakkar, 2017). Si un par de estudiantes trabajan en equipo construyendo los modelos de la izquierda y derecha de la figura 7 podrán darse cuenta que no es posible superponerlos.

Figura 7. Los objetos que pertenecen al grupo puntual D₂ son quirales (imágenes en el espejo no superponibles entre sí)

CONCLUSIÓN

Se ha descrito la construcción de un Visualizador Tridimensional de Operaciones de Simetría, VTOS, a partir de materiales de bajo costo. Asimismo, se propone su uso en la enseñanza y el aprendizaje de conceptos básicos de la simetría del grupo puntual D₂, para lo cual se recomienda aplicar la metodología presentada en este trabajo.

En su forma más simple y con propósitos de sustentabilidad, algunos de nuestros estudiantes optaron por dibujar los ejes sobre el modelo en lugar de representarlos físicamente. En ambos casos, una vez visualizados los ejes de rotación propia sobre él, les resultó más sencillo ubicarlos en las entidades químicas de la figura 1.

REFERENCIAS BIBLIOGRÁFICAS

Bogart, K. (2017). Groups acting on sets. In Combinatorics through guided discovery (pp. 103-132). Createspace Independent Publishing Platform.

Cotton, A. (1999). La Teoría de Grupos Aplicada a la Química. Limusa.

Cozzi, F., Powell, W. H., y Thilgen, C. (2005). Numbering of fullerenes (IUPAC recommendations 2004). Pure and Applied Chemistry, 77(5), 843-923. https://doi.org/10.1351/pac200577050843

Fuentes Cobas, L., y Fuentes Montero, M. (2008). La Relación estructura-simetría-propiedades en cristales y policristales (p. 40). Reverté.

Hargittai, M., y Hargittai, I. (2009). Symmetry through the eyes of a chemist. Springer Science & Business Media.

Pérez-Benítez, A. (2002). Ejemplificando la quiralidad con un clip. Educación Química, 13(1), 33-36. https://doi.org/10.22201/fq.18708404e.2002 .1.66316

Pérez-Benítez, A., y Arroyo-Carmona, R. E. (2003). Simetría para principiantes con un modelo octaédrico plegable. Educación Química, 14(4), 225-231. https://doi.org/10.22201/fq.18708404e.2003 .4.66230

Thakkar, A. (2017). Quantum chemistry: A concise introduction. Morgan & Claypool Publishers.

Tipler, P. A., y Mosca, G. (2006). Física para la ciencia y la tecnología. I. Mecánica, oscilaciones y ondas, termodinámica (p. 286). Reverté.

Willock, D. (2009). Molecular symmetry (pp. 25-44). John Wiley & Sons.