Innovación para la Enseñanza de la Química

SIMULACIONES PARA COMPLEMENTAR EL ESTUDIO DE LA CINÉTICA QUÍMICA A NIVEL BÁSICO

Sergio Baggio

Universidad Nacional de la Patagonia San Juan Bosco, Universidad Tecnológica Nacional Facultad Regional Chubut. Puerto Madryn, Argentina Email:

Email: baggiosergio@yahoo.com.ar

Recibido: 01/08/2020. Aceptado: 05/05/2021.

Resumen. La cinética química forma parte de la currícula de la mayoría de los cursos de química general que se dictan en las universidades. Su estudio presenta dificultades para los alumnos principiantes como se ha mostrado en muchas publicaciones de autores que han trabajado en el tema. En el presente trabajo se describen varios programas de simulación sobre cinética química, desarrollados por el autor y se discute la utilidad de las mismas para superar parcialmente las dificultades que presenta el tema en el proceso de enseñanza y de aprendizaje. Los programas pueden ser utilizados como actividades complementarias a las clases de laboratorio, problemas y teoría, contribuyendo de esa manera a la integración de éstas. Los programas han sido utilizados por el autor en el dictado de cursos de capacitación para docentes y alumnos de profesorado, recibiendo favorable acogida. Copia de los instalables de algunos de los programas, con sus guías para el alumno, están disponibles para los lectores interesados, sin cargo.

Palabras claves. simulaciones, química general, cinética química.

Simulations to complement the kinetics study in basical level

Abstract. Chemical kinetics is part of the curricula of most general chemistry courses that are taught in universities. Their study presents difficulties for beginners as shown in many publications of authors who have worked on the issue. In this paper the utility of simulations to partially overcome these difficulties in the teaching-learning process are discussed and various simulation programs on the subject, developed by the author are presented. Programs can be used as complementary laboratory classes activities, problems and theory, thus contributing to the integration of these. The programs have been used by the author in training courses for teachers and students of faculty, receiving favorable reception. A copy of the installable of some programs, with their guides for the student, are available to interested readers without charge.

Keywords. simulations, general chemistry, chemical kinetics.

INTRODUCCIÓN 

La cinética es parte de la ciencia del movimiento. Si bien en física hay una distinción entre dinámica y cinemática, en química esa distinción no existe. La cinética, en química, estudia la velocidad de las reacciones y los factores que la controlan, explicándolo a través de los mecanismos de reacción. La cinética difiere de la termodinámica como lo hace el aspecto dinámico del estático. Mientras la segunda se interesa sólo por el estado inicial y final del sistema, la cinética estudia el mecanismo por el cual se pasa de un estado al otro, considerando el tiempo requerido como un factor fundamental. La variable tiempo no es utilizada por la termodinámica, que se ocupa fundamentalmente de las condiciones en que se alcanza el equilibrio de una transformación. El equilibrio puede también ser abordado desde el punto de vista cinético, considerando el momento en el cual las velocidades de la reacción directa y opuesta se igualan. La inversa no es cierta: la velocidad de una reacción no puede ser entendida usando solamente argumentos termodinámicos (Frost y Pearson, 1961).

El estudio de la cinética química busca proporcionar información sobre cómo ocurren las reacciones químicas. Dichos estudios pueden dividirse en dos grupos. En el primero, las investigaciones abordan la construcción de modelos para describir y explicar las relaciones observadas entre la velocidad de reacción y las variables que ejercen influencia sobre ellas. También se ocupan del uso de tales modelos en el cálculo velocidad de reacción (Bykov, Elokhin, Gorban y Yablonskii, 1991). El segundo grupo de estudios busca proporcionar apoyo crítico para el mecanismo propuesto para cualquier reacción química. Esto se realiza principalmente mediante la recopilación de datos sobre los cambios en las variables que pueden usarse para expresar la velocidad a la que los reactivos se convierten en productos. Tales datos experimentales son integrados matemáticamente dando la ley de velocidad para esa reacción. Cualquier propuesta de mecanismo debe estar de acuerdo con la ley de velocidades (Blickensderfer, 1990). Sin embargo, esto no significa que se pueda deducir un mecanismo con certeza de los estudios cinéticos porque un mecanismo alternativo puede explicar los datos experimentales igualmente bien (Laidler, 1987, 1988).

Esta breve descripción del área señala su relevancia para una comprensión de importantes procesos químicos en la industria, medicina y áreas ambientales. Por ejemplo, en el proceso de producción de una determinada sustancia, ya sea en una industria o como parte del metabolismo humano, el conocimiento de la cinética química es de vital importancia.

Pasando a la enseñanza de la cinética, en el año 1976 Birk decía: “El estudio de la cinética en el laboratorio de química general ha sufrido de una escasez de experimentos sencillos e ilustrativos. Los experimentos de uso común no sirven para todos los criterios de un sistema ideal: (1) el sistema debe tener cierto interés intrínseco para los estudiantes; (2) el proceso debería hacerse lo suficientemente simple para ser entendido fácilmente; (3) los materiales utilizados deberían ser no tóxicos, no corrosivos y de bajo costo; (4) el aparato debería ser lo suficientemente simple como para que cada estudiante o grupo pequeño en una clase numerosa, pueda trabajar de forma independiente y sin la necesidad de recurrir a un equipo especial; (5) el sistema debe ser representativo de los sistemas reales que son comúnmente usados en los estudios cinéticos y deben dar resultados que sean al menos análogos a los datos reales”.

La situación parece no haber mejorado demasiado en este aspecto y por el contrario, con la disminución de horas de actividad práctica que se registra en la mayoría de los cursos universitarios, mayor conocimiento de los riesgos y presupuestos más exiguos, parece haberse profundizado.

A esto se suma que la cinética química es un tema complejo para los estudiantes principiantes que tienen reales dificultades para su aprendizaje (Kurt y Ayas, 2012). Esto se debe fundamentalmente a la escasez de reacciones relativamente simples, cuya cinética pueda estudiarse adecuadamente en una sesión de laboratorio, además del hecho de las dificultades que tienen los alumnos en la interpretación de los resultados experimentales cuando hay que obtener órdenes de reacción, energías de activación o propuestas de un mecanismo.

Ante la ausencia de un sistema químico que reúna todos los criterios mencionados por Birka, algunos autores se interesaron en el desarrollo de analogías para ilustrar algunos de los conceptos de la cinética. Así se propuso el estudio del enfriamiento de un líquido caliente o el calentamiento de un líquido frío, colocado en el medio ambiente, en función del tiempo (Birka, 1976). Con anterioridad Davenport, 1975 había descrito el estudio de flujo capilar como un análogo útil para el estudio de la cinética química. En años más recientes han aparecido otras publicaciones donde se trataron de utilizar analogías para facilitar el aprendizaje de la disciplina (Bender, Cutrera y Defago, 2007; Cortés, Pérez, López y Moore-Russo, 2011).

Las simulaciones también han sido propuestas como una alternativa para paliar el déficit que se ha comentado. El uso de las TIC en la enseñanza abre un abanico de nuevas posibilidades en la utilización de herramientas informáticas que rompen con esquemas tradicionales y revelan nuevas vías pedagógicas sustentadas en la participación activa de los estudiantes, lo que enriquece de manera notable el proceso de enseñanza y de aprendizaje (Uceda y Castañeda, 2015; Paredes y Molina, 2019). Uno de estos materiales que forman parte de los cambios históricos impuesto por la evolución tecnológica, que ha influido significativamente no solo en educación sino también en otros sectores como la medicina, la economía, la ingeniería, entre otras, es el uso y la implementación de los simuladores. Los simuladores utilizados en educación se definen como “programas que tienen un modelo de algún aspecto del mundo y que permite al estudiante cambiar algunos parámetros o variables de entrada, ejecutar el modelo y desplegar los resultados” (Escamilla, 2000).

Como un aporte adicional al desarrollo de simuladores para la enseñanza de la química que el autor ha implementado en los últimos años (Baggio, 2018, y referencias allí citadas), se presentan varios programas relacionados con la cinética química. Estos programas pretenden como objetivo, complementar las actividades de laboratorio que puedan hacerse sobre el tema y familiarizar al alumno con varios métodos experimentales de la cinética para que de esa manera pueda interpretar más fácilmente los resultados obtenidos y facilitar su manejo. Además, ésta complementación también se extiende a las clases de problemas donde es aun más evidente la falencia que muchos estudiantes principiantes presentan en la manipulación de los datos. La puesta a disposición de los programas a los docentes interesados permitirá expandir estos beneficios a otras escuelas y universidades.

En tiempos recientes con la aparición de la pandemia de Covid19, se ha debido recurrir al dictado de clases virtuales, donde este tipo de actividades tienen un rol preponderante.

DESARROLLO

El objetivo primero de estos simuladores es estudiar varias reacciones químicas, en estado gaseoso o solución, y encontrar la ley cinética que siguen. Se ha tratado de elegir reacciones donde la evolución de la misma se pueda seguir utilizando distintas metodologías, que ilustren cómo puede trabajarse en cinética en laboratorio. Así, en las simulaciones se siguen las reacciones utilizando cambios de volumen y/o cambios de presión, dilatometría, conductividad, colorimetría, entre otros. En todos los casos, los valores usados para concentraciones, temperaturas y constantes de velocidad fueron obtenidos de resultados experimentales citados en la literatura.

La expresión genérica para la velocidad de una reacción es:

v = k×[A]ⁿ¹×[B]ⁿ²_{… ,}

donde k es la velocidad específica de la reacción y los n_i, son los órdenes respecto de cada uno de los reactivos que influyen en la velocidad. La sumatoria de los n_i, da el orden total de la reacción.

Las reacciones simuladas son de primer o segundo orden, cosa que el alumno puede determinar haciendo un análisis adecuado de los resultados experimentales obtenidos. Para confirmar una reacción de primer orden se debería obtener una recta en la gráfica del Log[reactivo] en función del tiempo. Para segundo orden, la recta se obtiene cuando se grafica la inversa de la concentración, en función del tiempo. Para algunas reacciones puede trabajarse con las velocidades iniciales. La ejecución de la simulación, a dos temperaturas diferentes, permite estimar la energía de activación de la reacción estudiada. En efecto si se repite la experiencia a otra temperatura se puede determinar la velocidad específica k₂ a esa nueva temperatura y de acuerdo a Arrhenius

donde A es una constante, E_a la energía de activación de la reacción. Tomando logaritmos naturales,  Ln(k_i)=Ln(A)–E_a/RT . Planteando para cada T y restando nos queda

ln(k₁/k₂)= (E_a/R)×(T₁-T₂)/ T₁×T₂ (Chang, 2010)

A través de 5 programas diferentes se simula el estudio cinético de 7 reacciones:

1) SO₂Cl₂(g) ↔ SO₂(g)+Cl₂(g)

2) H₂O₂(ac) ↔ H₂O(l)+½ O₂(g)

3) 2 N₂O(g) ↔ 2 N₂(g)+O₂(g)

4) (CH₃)₂C(OH)CH₂COCH₃(l) ↔ 2 CH₃COCH₃ (l)

5)CH₃COOC₂H₅(ac)+Na⁺(ac)+OH^-(ac) ↔ CH₃COO^-(ac)+Na⁺(ac)+C₂H₅OH(ac)

6) Descomposición del violeta cristal en medio alcalino
7) H₂O₂(ac)+3 I^-(ac)+2 H₃O⁺(ac) ↔ 4 H₂O+I₃^-(ac)

Un programa desarrolla las primeras 3 reacciones y los 4 restantes cada una de las reacciones siguientes (4 a 7).

El seguimiento de cada reacción se realiza a través de medidas:

1 y 3) barométricas, 2) volumétricas, 4) dilatométricas, 5) conductimétricas, 6)fotométricas, 7)reacción tipo reloj.

Conjuntamente con los programas, el autor ha elaborado guías para el alumno, con un enfoque de investigación guiada, donde a través de preguntas se lo va orientando para la ejecución del mismo y la interpretación de los resultados. También, hay guías para el docente, donde se explica detalladamente el funcionamiento y los resultados esperables para las simulaciones.

Descripción de los simuladores:

1) Reacción:  SO₂Cl₂(g) ↔ SO₂(g)+Cl₂(g) (Smith, 1925)

Condiciones y velocidades específicas utilizadas

T = 593,1K   ; k = 0,001321min^-1

T = 602,4K   ; k = 0,002742min^-1

Las concentraciones permitidas para el SO₂Cl₂(g) son 0,02  y 0,14M

Figura 1. Corrida típica para la descomposición del SO₂Cl₂(g).

El programa registra la presión total del sistema gaseoso, a medida que avanza la reacción. A través de estos valores y la estequiometría, es posible calcular las presiones parciales de los participantes en la reacción. Una vez analizados los resultados experimentales, se concluye que la reacción es de primer orden. En la Figura 1 se muestra una corrida típica, en las condiciones que se muestran. Allí se observa la evolución de la P total en función del tiempo:

2) Reacción:H₂O₂(ac) 🡺 H₂O(l)+½ O₂(g) (Washburn, 2003)

Condiciones y velocidades específicas utilizadas:

T = 313,1K   ; k = 0,0079min^-1

T = 343,1K   ; k = 0,0588min^-1

Las concentraciones permitidas para el H₂O₂(ac) son 0,1 y 0,05M. Se supone que la presión atmosférica es de 760torr y el valor 100mL de la bureta coincide con el nivel del agua en la cuba neumática.

La reacción 2 se sigue volumétricamente, con un aparato como el que se muestra en la Figura 2, donde se muestra una corrida típica, en las condiciones que se indican en el dibujo.

Figura 2. Corrida típica de la descomposición del H₂O₂(ac).

La reacción es de primer orden. En este caso se trata de un experimento integrador, ya que para el cálculo de la presión a la cual está sometido el O₂ se requiere manejar el concepto de presión de vapor y leyes de los gases.

3) Reacción:  2 N₂O(g) ↔ 2 N₂(g)+O₂(g) (Hinshelwood, 1924)

Condiciones y velocidades específicas utilizadas:

T = 1030K    ; k = 0,77M^-1s^-1

T = 1085K    ; k = 3,93M^-1s^-1

Las concentraciones permitidas para el N₂O_(g) son 0,01 y 0,008M. La reacción ocurre en medio NaOH 0,4M.

En la simulación se utiliza un equipo semejante al de la reacción 1 y una corrida típica se muestra a continuación en la Figura 3.

Figura 3. Corrida típica de la descomposición del N₂O (g).

Como en el caso de la reacción 1, la presión total registrada y la estequiometría permiten calcular las presiones parciales de los participantes.

La reacción resulta de segundo orden.

4) Reacción:  (CH₃)₂C (OH) CH₂COCH₃ (l) ↔ 2 CH₃COCH₃ (l) (Karloff, 1927).

La reacción de descomposición del alcohol diacetónico se sigue por dilatometría, debido a la gran diferencia de densidad entre las dos sustancias: el alcohol diacetónico (ADA) 0,931 y la acetona 0,788g/mL. Se agregan 2,45 ó 4,90mL del alcohol (Mr=116,161g/mol) a una solución 2M de KOH, a fin de completar 50mL que se colocan en el dilatómetro. Se trabaja a 25°C y el aparato utilizado se muestra en la Figura 4:

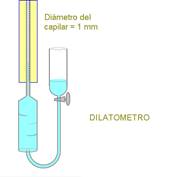
Figura 4. Aparato de dilatometría para estudiar la descomposición del ADA.

Los resultados de una corrida típica, con 2,45mL de alcohol  se muestran en la Tabla 1.

Tabla 1. Corrida típica en el dilatómetro para la descomposición del ADA.

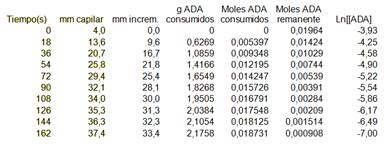
Se trata de una reacción de primer orden. En cada punto se puede calcular la cantidad de acetona como sigue: por cada gramo de descomposición del alcohol diacetónico, el volumen aumenta 0,143mL (0,931-0,788). Como el capilar es de 1mm² de sección, por cada 14,3mm de dilatación se forma 1g de acetona. En la Figura 5, se muestra la gráfica de Ln[ADA] en función del tiempo(s). La recta obtenida, confirma que se trata de una reacción de primer orden.

Figura 5. Gráfica del Ln[ADA] vs tiempo.

La pseudo constante de primer orden obtenida es k’ = 0,0183s^-1. Esta constante es k×[HO⁻]. La [HO⁻] se considera constante a lo largo de las experiencias. El orden respecto de la [ADA] puede obtenerse también a través de la velocidad inicial (Casado, López-Quintela, Lorenzo-Barral, 1986). En Figura 6, se muestran los gráficos de concentración vs tiempo (en segundos*0,1). Si se ajusta la curva con un polinomio (Baggio, 2011), por ejemplo de 3er grado, es posible calcular la velocidad inicial como la pendiente de la recta tangente a la curva en el punto t=0. Para ello se calcula el valor de la derivada de la curva en el punto de interés, cuyo valor resulta ser la pendiente de la recta en ese punto. Los valores -0,0033 y -0,0065mol/s que se obtienen y que coinciden con el coeficiente de primer orden del polinomio, muestran que la velocidad se duplica al duplicar la concentración inicial. Eso nos corrobora que en la expresión de la velocidad la [ADA] está a la primera potencia.

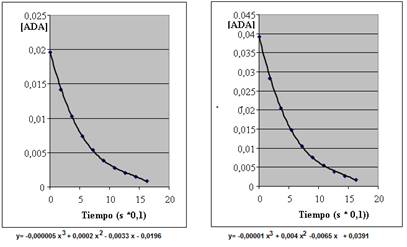
Figura 6. Gráficas de [ADA] vs. tiempo.

5)CH₃COOC₂H₅(ac)+Na⁺(ac)+OH^-(ac) ↔ CH₃COO^-(ac)+Na⁺(ac)+C₂H₅OH(ac)

(Findlay, 1955).

La cinética se sigue en este caso a través de medidas de conductividad. Inicialmente la conductividad del sistema estará dada por la conductividad del NaOH y al final por la del acetato de sodio e hidróxido, en caso que éste se encuentre en exceso. Se estudia la influencia de ambos reactivos y se utiliza el método de las velocidades iniciales. Se podrá trabajar a dos temperaturas diferentes para calcular energía de activación.

La conductancia específica de las soluciones fue estimadas a través de la ecuación y los parámetros que se dan en Dean (1985).

Para calcular la composición, conocida la conductancia específica, es una aproximación razonable suponer que las conductancias de los componentes se mantienen constantes en el rango de variación de concentraciones.

La celda utilizada tiene una constante igual a 1cm^-1, por lo que la inversa de la resistencia (que es lo que se mide en el puente de Wheastone) nos da la conductancia equivalente de la solución. Esta conductancia será  N_A×C_A + N_B×C_B donde N son normalidades y C conductancias específicas.

En la Figura 7 se muestra un croquis del puente de Wheastone utilizado. En el dibujo se indica R_x como la resistencia de la celda que se quiere determinar, siendo R₁, R₂ y R₃, resistencias de valores conocidos. Además, R₃ es una resistencia variable. Si la relación de las dos resistencias del brazo conocido (R₁/R₂) es igual a la relación de las dos resistencias del brazo desconocido (R_x/R₃), el voltaje entre los puntos medios será nulo y no circulará corriente entre los puntos C y B. Para efectuar la medida, se varía la resistencia R₃ hasta que no pase corriente por el galvanómetro.

En la condición de equilibrio se verifica que R_x = R₁×R₃/R₂.

Figura 7. Croquis del puente de Wheastone utilizado.

Una corrida típica se muestra en la Tabla 2, donde se indican los valores de conductividad específica obtenidas y las concentraciones calculadas, a largo del tiempo.

Tabla 2. Una corrida para concentraciones de acetato de etilo e hidróxido de sodio 0,01M a 25°C.

T = 25°C [Acetato etilo] = 0,0100 M [NaOH] = 0,0100 M
Tiempo (m)	[AcEt]	Cond.Esp (Ohm^-1cm)	Resistencia (Ohm)
0,00	0,0100	0,00236	445,6
1,80	0,0090	0,00221	474,2
4,05	0,0080	0,00207	507,5
6,95	0,0070	0,00192	546,4
10,80	0,0060	0,00177	592,5
16,21	0,0050	0,00162	647,7
24,31	0,0040	0,00147	715,3
37,82	0,0030	0,00131	799,8
64,83	0,0020	0,00116	908,5
145,87	0,0010	0,00100	1054,1
infinito	0,0000	0,00086	1219,5

La reacción resulta de segundo orden (primer orden en cada reactivo) con constantes: k₁₈ = 3,98 min^-1.M^-1, k₂₅ = 6,17min^-1.M^-1.

Para determinar el orden en cada reactivo se miden las velocidades iniciales. Para ello se grafican los puntos de concentración vs. tiempo y se ajusta un polinomio de grado 2 ó 3. Luego, se calcula la pendiente de la recta tangente en el punto t=0, cuyo valor resulta ser la velocidad inicial.

6) Descomposición del violeta cristal en medio alcalino (Corsaro, 1964).

La reacción puede representarse de la siguiente manera, donde se muestran también los colores de las soluciones de las especies intervinientes:

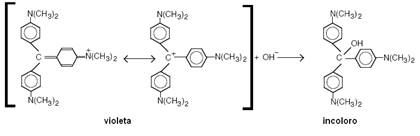
La contribución al híbrido de resonancia del violeta cristal (VC) de la segunda estructura en el corchete, sugiere una deficiencia de electrones en el C terciario y se esperaría un ataque por parte del ión hidróxido, formando el derivado carbinólico, que es incoloro, ya que se destruye la conexión de la conjugación entre los tres ciclos aromáticos.

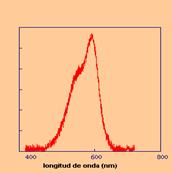
Figura 8. Espectro visible del Violeta Cristal.

En la Figura 8 se muestra el espectro de absorción en el visible del violeta cristal, con un máximo de absorción en 590nm. A esa longitud de onda, el coeficiente de extinción molar tiene valores dispares en la literatura. En la presente simulación se toma  ε= 7,55×10⁴ M^-1cm^-1.

La ley de velocidades es

V = k×[VC]×[HO⁻]

A fin de determinar el orden de reacción de cada reactivo, se procederá a trabajar con altas concentraciones de KOH (relativas al VC) para determinar el de este último y luego se repetirán experiencias variando la [HO⁻] para determinar el orden del mismo. Existe la posibilidad de trabajar a diferentes temperaturas para determinar la energía de activación de la reacción.

Durante las experiencias se seguirá la variación de la [VC], midiendo la absorbancia en un espectrómetro de doble haz, con celdas de paso=1 cm. Previamente se procederá a determinar la curva de calibración Absorbancia vs. [VC]. En cada experiencia de determinará k´= k×[HO⁻], de donde fácilmente se obtendrá k. En las experiencias cinéticas se tomarán 10mL de una solución de álcali que se diluyen a 50mL, con agua y por otro lado, se hace lo mismo con una solución  de VC de concentración 6,96 × 10^-5M. Las dos soluciones se mezclan, disparándose el reloj en ese momento. De esta operación resulta que tanto el álcali como el VC, se diluyen 10 veces. Los datos que utiliza el programa se listan a continuación (la concentración de KOH, es previa a la dilución) en la Tabla 3.

Tabla 3. Datos para el estudio cinético de la descomposición del VC.

	k´ = k×[HO^−]
KOH, M	25 °C	30 °C	35 °C	40 °C
0,033	0,0180	0,0263	0,0377	0,0535
0,050	0,0290	0,0399	0,0570	0,0828
0,083	0,0474	0,0651	0,0931	0,1334

Para determinar la curva de calibración se trabaja con una solución madre, cuya concentración, que se muestra en cada caso en el programa, varía entre ciertos valores. Se toman los volúmenes que se indican en la figura y se realizan las diluciones a 100mL:

Muestra:                 1      2       3      4       5      6       7       8

Los valores que se obtienen de Absorbancia, tanto en la calibración como en las cinéticas, se graban en un archivo de texto, llamado viol_res.txt. El archivo es de tipo “append”, por lo que se va grabando a continuación de lo ya existente, sin borrar lo anterior. A fin de evitar confusiones, antes de cada conjunto de datos se imprime la fecha y la hora. Resulta conveniente, cada tanto, limpiar el archivo.

Consideremos los valores a 40°C de las constantes de velocidad k’₁ y k’₃ resultan 0,1332 y 0,0533min^-1, respectivamente. Para el cálculo de k se procede así: la constante k’₃ resulta 0,0533min^-1. Como k’= k×[HO⁻], se determina k y el orden respecto del ion hidróxido haciendo los cocientes:

[HO⁻]₁/[HO⁻]₃ = 0,0083/0,0033 = 2,515; K’₁ /k’₃ = 0,1332/0,0533 = 2,50 lo que muestra que el exponente de la concentración de iones hidróxido debe ser 1. Con esto se determina la ley de velocidades, que a 40°C es:

V = k×[VC]×[HO⁻]

con k = 16,05 M^-1.min^-1.

En el cuadro se indican los valores de k a las otras temperaturas

Temperatura °C	25	30	35	40
k : M^-1.min^-1	5,71	7,37	11,22	16,05

Con los valores de k, a diferentes temperaturas, se puede calcular la energía de activación de la reacción, a través de la ecuación de Arrhenius.

7) Reacción:H₂O₂(ac)+3 I^-(ac)+2 H₃O⁺(ac) ↔ 4 H₂O+I₃^-(ac)(Shurvell, 1967)

La presente simulación muestra la determinación de la cinética de una reacción química, tipo reloj. Se trata de la simulación de la reacción entre el agua oxigenada, los iones yoduro y los iones hidronios, que reaccionan según:

H₂O₂(ac)+3 I^-(ac)+2 H₃O⁺(ac) ↔ 4 H₂O+I₃^-(ac)

La cinética de esta reacción es complicada y la ley de velocidades sugiere que la reacción puede proceder por dos caminos independientes (King, 1964):            d [I₃^-]/dt = k₂×[H₂O₂]×[I₃^-] + k₃×[H₂O₂]×[I₃^-]×[H₃O⁺]

Si los iones yoduro e hidronio, se encuentran inicialmente en gran exceso, su concentración se puede considerar constante a lo largo de toda la reacción, con lo que la ley de velocidades se transforma en:

d [I₃^-]/dt = k₁×[H₂O₂]  donde k₁ =k₂×[I₃^-] + k₃×[I₃^-]×[H₃O⁺]

En esta simulación se determinará k_1. Inicialmente se selecciona una temperatura. Pulsando sucesivamente las teclas superiores, a la derecha, se irán incorporando al recipiente de reacción el agua y las soluciones de KI, H₂SO₄, Na₂S₂O₃ y las gotas de almidón. Finalmente, se agrega el H₂O₂, cuya concentración real aparece en la ventana M real. Desde ese momento comienza a correr el reloj. Mientras aparezca el cartel “en ejecución” se deberá agregar solución de tiosulfato después de cada cambio de color. Se registran los tiempos en los cuales se producen estos.

En la Figura 9 se muestra una imagen de la pantalla donde se ven las teclas a las que se hacía referencia.

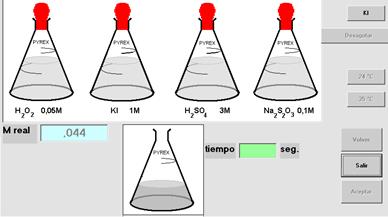
Figura 9. Pantalla del programa para realizar la reacción.

Una vez registrado todos los datos, se repite la reacción a la otra temperatura disponible. La reacción resulta de primer orden con respecto al agua oxigenada.

CONCLUSIONES

El uso de simulaciones se presenta como una interesante alternativa para complementar las actividades de laboratorio, teoría y problemas en los cursos de química general. En el caso particular de cinética química, algunos de los programas fueron utilizados corrientemente en nuestros cursos regulares de química general para la licenciatura de ciencias biológica en la UNPSJB. En particular las reacciones 2 y 6 fueron particularmente útiles para nuestros alumnos ya que les facilitan la comprensión de las actividades, que sobre esos temas, realizan en el laboratorio o clases de problemas. Al simular experiencias en el aula o en sus casas, que no ejecutaron en el laboratorio, se genera en muchos de ellos nuevas preguntas hacia los docentes, ampliando de esa manera la mejor comprensión del tema. Las actividades con simulaciones de prácticos de laboratorio se complementan en el proceso de aprendizaje, con la guía digital de problemas sobre el tema cinética química (Baggio, 2012) Paralelamente al uso en nuestros cursos, estos y otros programas son regularmente presentados por el autor en talleres que dicta en distintas universidades para profesores universitarios, alumnos de profesorado y docentes de escuela media, los cuales tienen generalmente una buena acogida. Los realizados durante los últimos años se listan en la bibliografía (Baggio, 2020).

Una copia de los instalables de algunos de los programas conjuntamente con las guías para el alumno se encuentra disponible, sin cargo, para los lectores interesados que se lo soliciten al autor por correo electrónico.

REFERENCIAS BIBLIOGRÁFICAS

Akerlof, G, (1927). Decomposition of Diacetone Alcohol Alkali Hydroxide Solutions, Journal of American Chemical Society, 49(12), 2955-2981

Baggio, S. (2018). Líquidos y soluciones: complementos informáticos para un curso de química general. Educación en la Química, 24(2), 137-154.

Baggio, S. (2020).  Simulaciones computacionales como estrategia para la enseñanza de la química, Taller de 24 hs en la Universidad Austral de Chile. Valdivia, Chile, 2018;   El Rol de los juegos en el aprendizaje de la química: Uso de herramientas informáticas para su implementación, REQ XVIII, Universidad Nacional del Rio IV, Rio IV, Córdoba, Agosto 2018; Las Simulaciones como un Elemento Integrador en Cursos de Química Básica Taller de 20 hs reloj, Universidad Nacional de la Patagonia Austral  Río Gallegos, Santa Cruz, Octubre 2019; Las Simulaciones como un Elemento Integrador en Cursos de Química Básica: Conferencia Virtual, Universidad Nacional de Costa Rica, Heredia, Costa Rica, Marzo 2020.

Baggio, S. (2011). Programa Aj_Pol_n. Resultados no publicados.

Baggio, S. (2012). Una guía digital de problemas para un curso de química general. Educación en la Química, 18(2),103-110.

Bender, G., Cutrera, G., y Defago, A. (2007). Cinética química y analogías: un análisis de las propuestas de enseñanza. I Jornadas de Enseñanza e Investigación Educativa en el campo de las Ciencias Exactas y Naturales, La Plata 18-19 de octubre de 2007.

Birk, J. B. (1976), Coffee Cup Kinetics, Journal Chemical Education, 53,3, 195-196.

Blickensderfer, R. (1990). Learning Chemical Kinetics with Spreadsheets. Journal of Computers in Mathematics and Science Teaching, 9,4, 35-43.

Bykov, V.I., Elokhin, V.I., Gorban, A.N., & Yablonskii, G.S. (1991). Kinetics models of catalytic reactions. En R.E. Compton (Ed.), Comprehensive chemical kinetics (pp. 47-81). Amsterdam: Elsevier.

Casado, J., López-Quintela, M.A., & Lorenzo-Barral, F.M. (1986). The initial rate method in chemical kinetics. Journal Chemical Education, 63, 450-451.

Chang, R. (2010). Química, McGraw-Hill.

Corsaro, G. (1964). A Colorimetric Chemical Kinetics Experiment. Journal Chemical Education, 41,1,48-50.

Cortés-Figueroa, J. E., Pérez, W. I., López, J. R. y Moore-Russo, D.A. (2011). An Analogy Using Pennies and Dimes to Explain Chemical Kinetics Concepts, Journal of Chemical Education, 88(7), 932-936.

Davenport, D. A. (1975), Capillary Flow, Journal Chemical Education, 52(6), 379-381.

Dean, J. A. (1985). Lange’s Handbook of Chemistry. Nueva York: McGraw Book Co.

Escamilla, J. (2000). Selección y uso de tecnología educativa. México: Trillas.

Findlay, A. (1955). Prácticas de Físicoquimica. Buenos Aires: Editorial Médico-Quirúrgica.

Frost, A. A. y  Pearson, R. G. (1961). Kinetics and Mechanism. Nueva York: John Wiley & Sons.

Hinshelwood, C. N. y Burk, R. E. (1924). The homogeneous thermal decomposition of nitrous oxide. Royal Society of London, 106, 284-291.

King, E. L. (1964). How Chemical Reactions Occur. Nueva York: W. A. Benjamin.

Kurt, S. y Ayas, A. (2012). Improving students’ understanding and explaining real life problems on concepts of reaction rate by using a four step constructivist approach, Turkey, Energy Education Science and Technology Part B: Social and Educational Studies, 4(2), 979-992.

Laidler, K. J. (1988). Rate-controlling step: A necessary or useful concept? Journal Chemical Education, 65, 250-254.

Laidler, K. J. (1987). Chemical kinetics. Nueva York: Harper & Row.

Paredes, J. y Molina, M. (2019). Enseñanza de la cinética química por medio de simulaciones y aprendizaje activo. Tecné, Episteme y Didaxis, 45, 71-88.

Shurvell, H. F. (1967).  The kinetics of an ionic reaction, Journal Chemical Education, 44(10), 577-578.

Smith, D. F. (1925). The rate of thermal decomposition of sulfuryl chloride. a first-order homogeneous gas reaction. Journal of American Chemical Society, 47(7), 1862–1875.

Useda, P. L. y Castañeda, M. A. G. (2015). El ambiente digital en la comunicación, la actitud y las estrategias pedagógicas utilizadas por docentes. Tecné, Episteme y Didaxis, 37, 109-129.

Washburn, E. W. (2003). International Critical Tables. Knovel.